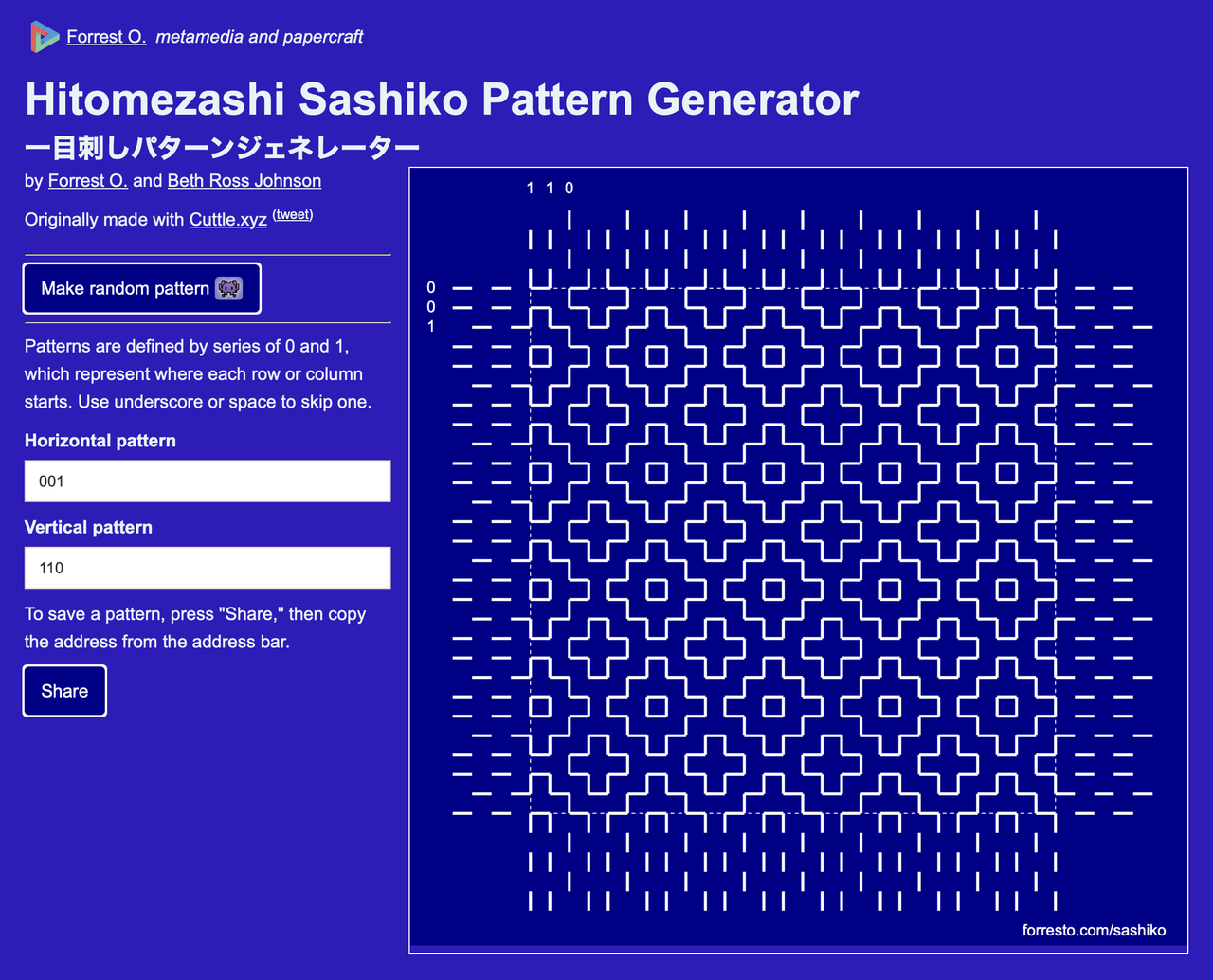
Sashiko design app
I took a mending class with Beth Johnson and was drawn to Hitomezashi Sashiko which are patterns made by offsetting rows and columns of stitches by 0 or 1 stitch length. As a programmer I challenged myself to stay AFK during the class, but after the class I had to experiment with programming some visualizations of the patterns. I made this in collaboration with Beth, who also weaves these patterns, which is called Sashiko Ori.
Niche tools for craft design
I started experimenting in Cuttle, and then made a stand-alone web app:

Examples of the weaving output from my co-author. North House Folk School interview with Beth, with some more examples of the weaving.
Beth has used the app in classes and workshops. It's cool to see weavers experimenting and iterating on patterns on their own devices. Some people had the idea of encoding text to binary, to put secret messages into the pattern.

This experience confirms that there is a big unmet demand for niche design tools for craftspeople. I'd like to do more collaborations like this. I think that folk schools, community collages, and fab labs are fertile grounds for this code + craft collaboration.
I'm working on Cuttle.xyz, and part of our mission is to make it more accessible to build parametric design tools like this.
How many?
In a workshop, Beth was asked how many patterns are possible to make with our app.
I think it's 2^(warp+weft), so... a comically huge number of possibilities. The app has 28 rows and columns available, so 2^56, about 72 quadrillion. Animating through every option at 60 frames per second, it would take 38 million years to see them all.

By limiting the pattern to 4x4, I see 2^8 unique patterns, 256. My theory is that the repeating patterns are included in the list of every pattern, which can be enumerated by binary numbers like this. Is there a way to prove that the patterns are unique?
Replies
- ← Previous
Sierpiński curve animation - Next →
2023 Studio Wall (annotated)